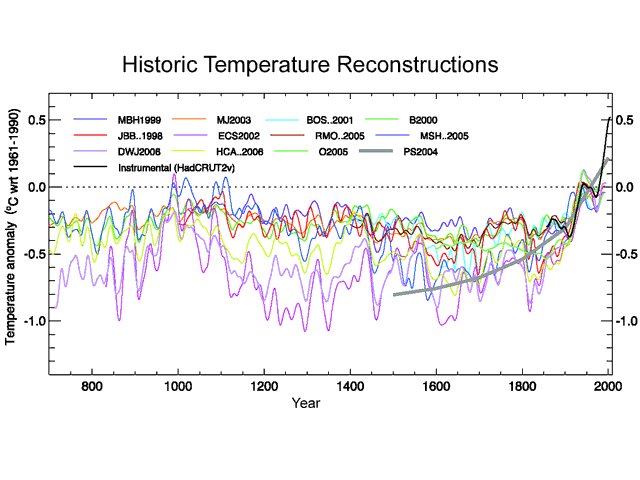
I have posted many times on the numerous problems with the historic temperature reconstructions that were used in Mann’s now-famous "hockey stick."   I don’t have any problems with scientists trying to recreate history from fragmentary evidence, but I do have a problem when they overestimate the certainty of their findings or enter the analysis trying to reach a particular outcome.   Just as an archaeologist must admit there is only so much that can be inferred from a single Roman coin found in the dirt, we must accept the limit to how good trees are as thermometers.  The problem with tree rings (the primary source for Mann’s hockey stick) is that they vary in width for any number of reasons, only one of which is temperature.

One of the issues scientists are facing with tree ring analyses is called "divergence."  Basically, when tree rings are measured, they have "data" in the form of rings and ring widths going back as much as 1000 years (if you pick the right tree!)  This data must be scaled — a ring width variation of .02mm must be scaled in some way so that it translates to a temperature variation.  What scientists do is take the last few decades of tree rings, for which we have simultaneous surface temperature recordings, and scale the two data sets against each other.  Then they can use this scale when going backwards to convert ring widths to temperatures.

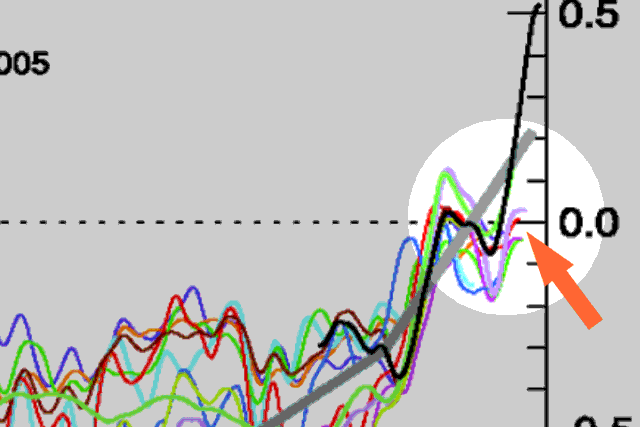
But a funny thing happened on the way to the Nobel Prize ceremony.  It turns out that if you go back to the same trees 10 years later and gather updated samples, the ring widths, based on the scaling factors derived previously, do not match well with what we know current temperatures to be. 

The initial reaction from Mann and his peers was to try to save their analysis by arguing that there was some other modern anthropogenic effect that was throwing off the scaling for current temperatures (though no one could name what such an effect might be).  Upon further reflection, though, scientists are starting to wonder whether tree rings have much predictive power at all.  Even Keith Briffa, the man brought into the fourth IPCC to try to save the hockey stick after Mann was discredited, has recently expressed concerns:

There exists very large potential for over-calibration in multiple regressions and in spatial reconstructions, due to numerous chronology predictors (lag variables or networks of chronologies – even when using PC regression techniques). Frequently, the much vaunted ‘verification’ of tree-ring regression equations is of limited rigour, and tells us virtually nothing about the validity of long-timescale climate estimates or those that represent extrapolations beyond the range of calibrated variability.

Using smoothed data from multiple source regions, it is all too easy to calibrate large scale (NH) temperature trends, perhaps by chance alone.

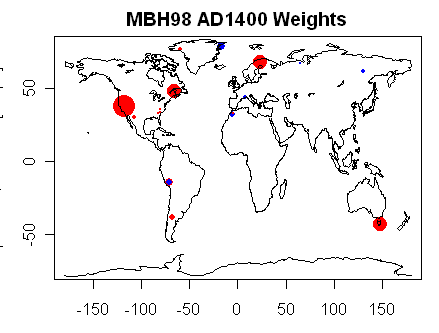
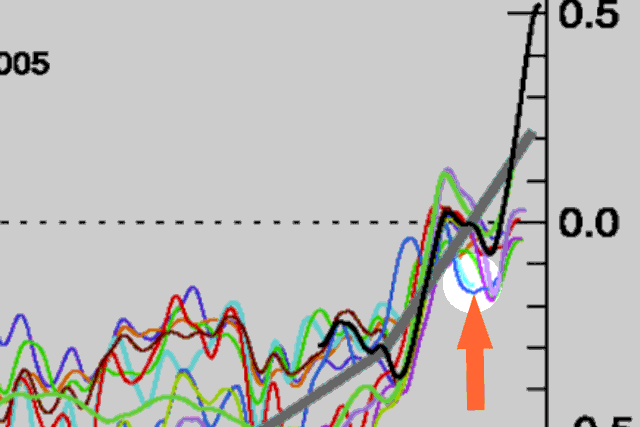
But this is what really got me the other day.  Steve McIntyre (who else) has a post that analyzes each of the tree ring series in the latest Mann hockey stick.  Apparently, each series has a calibration period, where the scaling is set, and a verification period, an additional period for which we have measured temperature data to verify the scaling.  A couple of points were obvious as he stepped through each series:

1. Each series individually has terrible predictive ability.  Each were able to be scaled, but each has so much noise in them that in many cases, standard T-tests can’t even be run and when they are, confidence intervals are huge.  For example, the series NOAMER PC1 (the series McIntyre showed years ago dominates the hockey stick) predicts that the mean temperature value in the verification period should be between -1C and -16C.  For a mean temperature, this is an unbelievably wide range.  To give one a sense of scale, that is a 27F range, which is roughly equivalent to the difference in average annual temperatures between Phoenix and Minneapolis!  A temperature forecast with error bars that could encompass both Phoenix and Minneapolis is not very useful.
2. Even with the huge confidence intervals above, the series above does not verify!  (the verification value is -.19).  In fact, only one out of numerous data series individually verifies, and even this one was manually fudged to make it work.

Steve McIntyre is a very careful and fair person, so he allows that even if none of the series individually verify or have much predictive power, they might when combined.  I am not a statistician, so I will leave that to him to think about, but I know my response — if all of the series are of low value individually, their value is not going to increase when combined.  They may accidentally in mass hit some verification value, but we should accept that as an accident, not as some sort of true signal emerging from the data. 

Posting has been light, because I have been very busy at work and because I just have not seen that much science of late that was interesting to report, and there is only so much of the political yada yada on the subject of climate I can stomach.

But I learned something the other day in this post by Steve McIntyre.  He as a nice way of cutting through all the BS about various statistical transforms that are used to create Mann’s hockey stick chart when he writes:

Whenever there is any discussion of principal components or some such multivariate methodology, readers should keep one thought firmly in their minds: at the end of the day – after the principal components, after the regression, after the re-scaling, after the expansion to gridcells and calculation of NH temperature – the entire procedure simply results in the assignment of weights to each proxy. This is a point that I chose to highlight and spend some time on in my Georgia Tech presentation. The results of any particular procedural option can be illustrated with the sort of map shown here – in which the weight of each site is indicated by the area of the dot on a world map. Variant MBH results largely depend on the weight assigned to Graybill bristlecone chronologies – which themselves have problems (e.g. Ababneh.)

In effect, while Mann used 50,60 proxy sets, just four determined about 90% of the answer.  Often, Mann has been challenged by historians who argue that the historical written record stands in opposition to his proxy work, since the historical record is clear about a Medieval warm period (where grapes were grown further north than they are today and Greenland was green) and a little ice age (where rivers froze that seldom froze before or since).  Mann has always responded that written records are limited to Europe and north Africa, while his hockey stick is global, but this chart tends to put the lie to that assertion.  And that is before we even discuss how bad trees are as thermometers.

While I am big proponent of the inherent superiority of satellite temperature measurement over surface temperature measurement (at least as currently practiced), I have argued for a while that the satellite and surface temperature measurement records seem to be converging, and in fact much of the difference in their readings is based on different base periods used to set the "zero" anomoly. 

I am happy to see Anthony Watt has done this analysis, and he does indeed find that, at least for the last 20 years or so, that the leading surface and satellite temperature measurement systems are showing about the same number for warming (though by theory I think the surface readings should be rising a bit slower, if greenhouse gasses are the true cause of the warming).  The other interesting conclusion is that the amount of warming over the last 20 years is very small, and over the last ten years is nothing.

I am taking a course in the history of the High Middle Ages in Europe, say between 1000AD and 1300.  One of the demographic drivers of the Middle Ages is the fact that population, while flat before 1000 and declining after 1300, actually doubled in Europe between 1000 and 1300.  One of the key drivers was a very warm period that caused agriculture to flourish.

The funny part was listening to the professor try to present this section to today’s audience.  He had to keep saying "I know you may find this hard to believe, but warming was very beneficial to European civilization."  It was clear the audience was so programmed to think warming=bad, that listeners had a hard time accepting the historical fact that warming created a boom, including a population boom, in Middle Age Europe.

OK, I would have assumed that the title for this post was obvious to all:  There are a lot of reasons that trees don’t make very good thermometers.  Now, that is not a criticism of climate archaeologists who use tree rings to infer the historical temperature record.  Sometimes, we have to work with what we have.  Historians are the first to admit that coins are not the best way to deduce history, but sometimes coins are all we have.

But when historians rely on imperfect evidence, there generally is an understanding that the historical record created from this evidence is tentative and subject to error.  Unfortunately, some climate scientists have lost this perspective when it comes to tree-ring analyses, such as Mann’s hockey stick.  They tend to bury the fact that:

“There are reasons to believe that tree ring data may not capture long-term climate changes (100+ years) because tree size, root/shoot ratio, genetic adaptation to climate, and forest density can all shift in response to prolonged climate changes, among other reasons.” Furthermore, Loehle notes “Most seriously, typical reconstructions assume that tree ring width responds linearly to temperature, but trees can respond in an inverse parabolic manner to temperature, with ring width rising with temperature to some optimal level, and then decreasing with further temperature increases.” Other problems include tree responses to precipitation changes, variations in atmospheric pollution levels, diseases, pest outbreaks, and the obvious problem of enrichment that comes along with ever higher levels of atmospheric carbon dioxide. Trees are not simple thermometers!

When the tree-ring folks like Mann first did their analyses, they calibrated tree ring growth over recent decades with the recent historical temperature record, and then projected this calibration backwards on history.  But, as noted in the quote above, there is a lot of evidence that these calibration factors may not be linear over time.  And in fact, the few people that have gone back and resampled Mann’s trees have found that their growth diverges substantially from predicted values – in other words, the relationship between tree ring growth and temperature is not constant. 

Now, this does not make Mann and his peers bad scientists.  They were trying their best to reconstruct history, they tried one methodology, but then evidence mounted that this methodology is flawed.  What makes them potentially bad scientists is their reaction to the negative evidence.  Once evidence of the divergence problem was raised, scientists have simply ceased resampling trees.  Their focus hs become defending their original approach, rather than improving it based on new information.

Often, new approaches require new people, as in this case:

Loehle gathered as many non-tree ring reconstructions as possible for places throughout the world (Figure 1). There are dozens of very interesting ways to peer into the climatic past of a location, and Loehle included borehore temperature measurements, pollen remains, Mg/Ca ratios, oxygen isotope data from deep cores or from stalagmites, diatoms deposited on lake bottoms, reconstructed sea surface temperatures, and so on. Basically, he grabbed everything available, so long as it did not rely on trees.

And he got this plot for a temperature reconstruction:

Only time will tell if this approach holds up better than tree rings, but it does better match the annecdotal history we have, including a Medieval warm period where Greenland was, you  know, green and a little ice age in the 17th century.  Like Mann, Loehle’s first version had some statistical and procedural errors.  Unlike Mann, Loehle reworked the whole analysis when these errors were pointed out.

New study conducted in California (emphasis added):

We investigated air temperature patterns in California from 1950 to 2000. Statistical analyses were used to test the significance of temperature trends in California subregions in an attempt to clarify the spatial and temporal patterns of the occurrence and intensities of warming. Most regions showed a stronger increase in minimum temperatures than with mean and maximum temperatures. Areas of intensive urbanization showed the largest positive trends, while rural, non-agricultural regions showed the least warming. Strong correlations between temperatures and Pacific sea surface temperatures (SSTs) particularly Pacific Decadal Oscillation (PDO) values, also account for temperature variability throughout the state. The analysis of 331 state weather stations associated a number of factors with temperature trends, including urbanization, population, Pacific oceanic conditions and elevation. Using climatic division mean temperature trends, the state had an average warming of 0.99°C (1.79°F) over the 1950–2000 period, or 0.20°C (0.36°F) decade.

Southern California had the highest rates of warming, while the NE Interior Basins division experienced cooling. Large urban sites showed rates over twice those for the state, for the mean maximum temperatures, and over 5 times the state’s mean rate for the minimum temperatures. In comparison, irrigated cropland sites warmed about 0.13°C [per decade] annually, but near 0.40°C for summer and fall minima. Offshore Pacific SSTs warmed 0.09°C decadefor the study period.

So, warming has occured mainly in the urban areas, while the least developped regions have cooled.  Increase of minimum temperatures rathern than daily maximum’s could be a result of CO2, but is more likely a signature of urban heat islands.  In particular, look at Anthony’s map in the linked article.  Notice the red dots for hotter areas and the cool dots for cooler areas.  The red dots are all on… cities.  The blue dots are all in the countryside.  You make the call — urban heat or greenyhouse effect.

Over the last several years, there has been quite a bit of debate in climate
circles over historical temperature reconstructions from various "proxies" like
ice cores and tree ring widths.  The debate really heated up a few years back
when Michael Mann introduced, and the climate catastrophists at the UN IPCC
adopted, the hockey stick chart.  Until that time, both scientists and
historians agreed that there was good evidence for a period in the Middle Ages
with temperatures as warm or warmer than today (thus the name "Greenland" and
not "Glacierland") and a period known as the Little Ice Age in the 17th to 19th
centuries that was quite frosty.  Mann attempted to refute this view, using data
mainly from bristlecone pine tree rings, that the temperature history over the
last 1000 years was in fact quite stable, at least until man started producing
CO2.  (I was not writing on climate at the time, but I always wondered if any
editor availed himself of the "Mann blames Man" headline.)

But why do these temperature reconstructions matter?  Aren’t we more
concerned with the temperature in 2050 than in 1050?  Yes and no.  To really do
any kind of job at predicting future temperatures, we need more than egghead
computer models tweaked in some scientist’s office.  What we really need are
good empirical studies about the sensitivity of temperature to different
variables.

We can see the importance of historical proxies in the recent study by
Scafetta and West (pdf) which looked at historical correlations between solar
activity and temperatures.  The authors performed their analysis multiple times,
both using "flat" historical reconstructions like Mann’s and other
reconstructions (e.g. Moberg)
which show more historical variability.  The authors concluded (emphasis
added):

Climate is relatively insensitive to solar changes if a
temperature reconstruction showing little preindustrial variability is adopted.
In this scenario most of the global warming since 1900 has to be interpreted as
anthropogenically induced. On the other hand, if a secular temperature
showing large preindustrial variability is adopted, such as MOBERG05, the
climate is found to be very sensitive to solar changes and a significant
fraction of the global warming that occurred during last century should be solar
induced. If ACRIM satellite composite is adopted the Sun might have
further contributed to the recent global warming.

Some thoughts:

• So, which results should we rely on?  The ones using Mann’s data
  or the ones using Moberg’s?  Well, even the catastrophists at the IPCC have
  abandoned Mann in favor of Moberg, so one should assume the conclusions in bold
  are very much in play.
• Either way, don’t panic!  Even if all the 0.6C warming in the last century was due to CO2, simple math says that we should not expect more than about 1 degree more warming over the next century  (calculation here).  If the sun caused half of that 0.6C, then you can cut future warming forecasts in half.
• Mann’s work is full of errors, both statistical and otherwise.  Beginning with McIntyre and McKittrick, and proceeding to many major scientists, his work has been discredited, though he does keep trying to save the thin branch (probably from a bristlecone pine!) he has crawled out on, but he refuses to fix even basic scribal errors pointed out in his first study.  I discuss more of the problems with Mann and other similar proxy studies, including the divergence problem, here.
• Both CO2 Science and Climate Audit have more on historical proxy studies and their problems than you can ever digest.
• Though it doesn’t make the front pages, there are still good common sense peer-reviewed studies that show the Medieval Warm Period and Little Ice Age that we could expect from narrative historical records.  One such is Loehle, Via Climate Audit  (temperature anomaly over last 2000 years or so, via proxies):

• Steven Milloy, via Tom Nelson, has much more on the sun as the primary driver of climate.
• You can view the section of my global warming film on historical proxies below.  The proxy part starts around 3:00 minutes in (or -5:30 from the end if it is shown that way)

Loehle, Via Climate Audit  (temperature anomaly over last 2000 years or so, via proxies):

If your are interested in temperature proxies, check out the CA post.  It has what I have never seen before, a gallery of graphs of all the individual proxies that go into the summary/average above.  Lots of noise is my chief observation.

To some extent, 1000-year temperature histories are moderately irrelevent to modern global warming discussions.  In fact, it is fairly amazing that the evidence of tree rings and such over 1000 years is discussed more than the instrumental record of the last 100, which tends to undercut most catastrophic warming forecasts.  However, catastrophists have attempted to use these past temperature reconstructions to make the argument that temperatures were incredibly stable and low right up to the point that man has made them higher and less stable in the last 100 years.  For this reason it is worth discussing them, if only to refute this conclusion.

I won’t go into a lengthy discussion of historical reconstructions, as I alread have in my book and in my movie (both free online).  In this post I just want to talk about one issue:  the splice.

Below is the 1000-year temperature reconstruction (from proxies like tree rings and ice cores) in the Fourth IPCC Assessment.  It shows the results of twelve different studies, one of which is the Mann study famously named "the hockey stick."

Among many issues, I pointed out the fact that this chart appends or splices the black line, actual measured temepratures, onto the colored lines, which are the historical temperature reconstructions from proxies. 

I made the point that this offended by scientific training:  When one gets an inflection point right at the place where two data sources are spliced, as is the case here, one should be suspicious that maybe the inflection is an artifact of mismatches in the data sources, and not representative of a natural phenomenon.  And, in fact, when one removes the black line from measured temperatures and looks at only proxies, the hockey stick shape goes away:

The other day I discovered that this inflection point is a fairly old criticism (no surprise, I never claim to be original).  Old enough, in fact, that Michael Mann and the folks at realclimate.org have fired back:

No researchers in this field have ever, to our knowledge, "grafted the thermometer record onto" any reconstruction. It is somewhat disappointing to find this specious claim (which we usually find originating from industry-funded climate disinformation websites) appearing in this forum.

The guys at realclimate are just so cute with the "industry-funded climate disinformation" attack — they remind me of the Soviets and how they used to blame everything on CIA plots.  I can say that 1) I recognized this problem on my very own after about 20 seconds of looking at the graph and 2) I have yet to recieve my check from the industry cabal.

It turns out, however, that this is wildly disingenuous.  What they mean is that none of the colored lines include gauge measures grafted onto older proxy data.  But I never really accused them of that.  Interestingly, Steve McIntyre argues that even this claim is wrong, and some of the colored lines do include spliced-on gauge measures.

But my point, which Mann has never refuted or addressed, is that whether the proxy lines themselves include grafted data or not, the proxy lines are NEVER shown to the public or to policy makers without the gauge temperature line added to the chart.  Have you ever seen the proxy lines as they are in my third chart above without the 20th century gauge temperature line?  If in policy discussions and media reports, this gauge temperature line is always included on the graphs in a way that it looks like an extention of the proxy series, then effectively they are grafting the data sets together in every discussion that really matters.

By the way, it is fairly easy to demonstrate that the proxy studies and the gauge temperature measurements do not represent consistent and therefore mergeable data sets.  Over hundreds of years, we have developped a lot of confidence that the linear thermal expansion of mercury in a glass tube is a good proxy for temperatures.  We have not, however, developped similar confidence in bristle cone pine tree rings, whose thickness can be influenced by everything from soil and atmospheric composition to precipitation.  Lets look at a closeup of the graph above:

You can see that almost all of the proxy data we have in the 20th century is actually undershooting gauge temperature measurements.  Scientists call this problem divergence, but even this is self-serving.  It implies that the proxies have accurately tracked temperatures but are suddenly diverting for some reason this century.  What is in fact happening are two effects:

1. Gauge temperature measurements are probably reading a bit high, due to a number of effects including urban biases
2. Temperature proxies, even considering point 1, are very likely under-reporting historic variation.  This means that the picture they are painting of past temperature stability is probably a false one.

All of this just confirms that we cannot trust any conclusions we draw from grafting these two data sets together.

By the way, here is a little lesson about the integrity of climate science.  See that light blue line?  Here, let’s highlight it:

For some reason, the study’s author cut the data off around 1950.  Is that where his proxy ended?  No, in fact he had decades of proxy data left.  However, his proxy data turned sharply downwards in 1950.  Since this did not tell the story he wanted to tell, he hid the offending data by cutting off the line, choosing to conceal the problem rather than have an open scientific discussion about it.

The study’s author?  Keith Briffa, who the IPCC named to lead this section of their Fourth Assessment.

More discussion on this topic can be found in my book and in my movie (both free online). 

Many of you have probably read about the disputes over temeprature histories like Mann’s hockey stick chart.  I thought you might be interested in how some of these 1000-year long proxies are generated.  There are several different approaches, but one that Mann relied a great deal on is measuring tree rings in bristle cone pine trees.  Here is a picture of a researcher taking a core from a very old tree that is then sent to a lab to have it’s ring widths measured. 

In theory, these ring widths are directly proportional to annual temepratures, but there are a lot of questions about whether this is really true.  Other factors, like changing precipitation patterns, might also affect ring widths, and there may be reasons why the scale could change over time.  Remember, we only have a few decades, at most, of good temperature data to scale growth in a tree that goes back over a thousand years.  In fact, scientists are finding that, more recently, tree ring proxy data for current growth is diverging from surface temperature data, meaning either that surface temperature data is flawed or that they don’t really understand how to scale tree ring data yet.  Interestingly, and as a sign of the health of climate science, researchers have reacted to this problem by … not updating tree ring proxy databases for recent years.  That’s one way to handle data that threatens your hypothesis — just refuse to collect it.  Much more on proxy histories here.

On this blog and at Coyote Blog, we have focused a lot of attention on the adjustment processes used by NOAA and James Hansen of NASA’s GISS to "correct" historical temperatures.  Steve McIntyre has unearthed what looks like a simply absurd example of the lenghts Hansen and the GISS will go to tease a warming signal out of data that does not contain it. 

The white line is the measured temperatures in Wellington, New Zealand before Hansen’s team got hold of the data.  The red is the data that is used in the world-wide global warming numbers after Hansen had finished adjusting it.  The original flat to downward trend is entirely consistent with sattelite temeprature measurement that shows the southern hemisphere not to be warming very much or at all.

What do these adjustments imply?  Well, Hansen has clearly reduced temperatures down in the forties while keeping them about the same in 1980.  Why?  Well, the only possible reason would be if there was some kind of warming bias in 1940 in Wellington that did not exist in 1980.  It implies that things like urban effects, heat retention by asphalt, and heat sources like cars and air conditioners were all more prevelent in 1940 New Zealand than in 1980.  However, unless Wellington has gone through some back to nature movement I have not heard about, this is absurd.  Nearly without exception, if measurement points experience changing biases in our modern world, it is upwards over time with urbanization, not downwards as implied in this chart.

Postscript:  A perceptive reader might ask whether Hansen perhaps has specific information about this measurement point.  Maybe its siting has improved over time?  However, Hansen has to date absolutely rejected the effort made by folks like surfacestations.org to document specific biases in measurement sites via individual site surveys.  Hansen is in fact proud that he makes his adjustments knowing nothing about the sites in question, but only using statistical methods (of very dubious quality) to correct using other local measurement sites. 

Last week we saw how Antarctic ice is advancing, but somehow this never makes the news despite huge coverage of Arctic ice retreats.

One good reason for this may well be that there has been no measured warming in Antarctica over the last 50 years.

Steve McIntyre summarizes

As I’ve discussed elsewhere (and readers have observed), IPCC AR4 has some glossy figures showing the wonders of GCMs for 6 continents, which sounds impressive until you wonder – well, wait a minute, isn’t Antarctica a continent too? And, given the theory of “polar amplification”, it should really be the first place that one looks for confirmation that the GCMs are doing a good job. Unfortunately IPCC AR4 didn’t include Antarctica in their graphics. I’m sure that it was only because they only had 2000 or so pages available to them and there wasn’t enough space for this information.